Questions asking for an explanation can typically be answered
in 1-2 sentences, 3 at most. You may also write out some mathematics
to go with your explanation. It may be helpful to "explain"
your answers as if you were studying with a friend. Don't
spend too much time on any one question. Answer as best you
can and move on. Partial credit may be assigned.
| 1. |
(4 pts) Solve.
8-(x-3)+ 5x = 2(-1 + 2x)
+ 13 + x
|
_______________________
|
| 2. |
(2 pts) Which number shown on the number line below
has the largest absolute value? _______
(3 pts) Explain your reasoning.
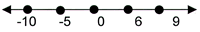
|
| 3. |
(5 pts) Solve.
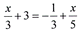
|
_______________________
|
| 4. |
John was asked to find any like terms in the question
below.
(2 pts) Circle like terms. 8xy2
- 2xy - 3xy2 + 5x2y
- 7x2 + 12y2
+ 8
(3 pts) What is meant by "like terms"?
|
| 5. |
(4 pts) Solve.
2(2 - x) > -2
|
_______________________
|
| 6. |
Alice was asked to solve the equation 2x
- 6 = 15 - x. Alice said the solution is 7.
(2 pts) What does it mean to "solve" an equation?
(1 pt) Did Alice solve this equation correctly? Circle
Yes or No.
(2 pts) Explain how you arrived at your conclusion.
|
| 7. |
(5 pts) Simplify completely.
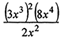
|
_______________________
|
| 8. |
A friend asked Sue to factor x2
- x - 6.
(4 pts) What does the word "factor" mean?
|
| 9. |
(4 pts) Factor completely.
4x2 + 9x + 5
|
_______________________
|
| 10. |
Three friends are studying the three forms of linear
equations shown below.
Slope-intercept: y= mx + b
Point-slope: y - y1 = m(x
- x1)
Standard: Ax + By = C
| A study question asks them to graph
the equation |
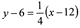 |
, which is in point-slope form. |
Curly says that he is going to leave it in point-slope
form, then graph it.
Larry says that he is going to write it in slope-intercept
form, then graph it.
Moe says that he is going to write it in standard
form, then graph it.
(2 pts) Assuming that they do not make any mistakes
in constructing their graphs, and without trying it
all three ways yourself, is it possible to know if their
graphs will look the same?
Circle Yes or No.
(3 pts) Provide an explanation that supports your
choice.
|
| 11. |
(4 pts) Solve. Show your work using algebra.
x2 + 6 = 5x
|
_______________________
|
| 12. |
(4 pts) A friend studying solving inequalities is asked
to solve -4x < 12. She correctly writes
the following steps:
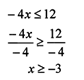
Explain why it is necessary
to change the direction of the inequality in this case.
|
| 13. |
(4 pts) Simplify completely by rewriting as a single
fraction.
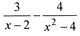
|
_______________________
|
| 14. |
(4 pts) Melissa is asked to add the fractions below.
| a) |
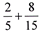 |
b) |
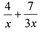 |
Melissa tells her friend Jennifer that she knows how
to do the problem in part (a), but that she has no clue
how to do the problem in part (b). Show Melissa how
to do the second problem and explain how the second
problem is similar to the first problem.
|
| 15. |
(5 pts) The width of a rectangle is three inches less
than twice the length. The perimeter is 54 inches. Using
algebra, show the necessary steps to find the dimensions
of the rectangle. No credit will be given unless the
work is shown using algebra.
Width = ____________
Length = ____________
|
| 16. |
A question asks Harry to circle the true statement(s)
below.
(2 pts) Which statement(s) should Harry circle?
x3 = 3·3·3
3x =x·x·x
x3 = x·x·x
3x = x·x
· ... · x (there are an unknown
number of x's on the right side)
(3 pts) Provide an explanation that supports your
choice.
|
| 17. |
(5 pts) Find the equation of the line through the points
(-6, 16) and (3, 4). Write your final in the form y
= mx + b.
|
_______________________
|
| 18. |
Edith is given the graph below. She is asked to find
the y-intercept and the slope. Find these,
if there is enough information given. Otherwise write
"not enough information".
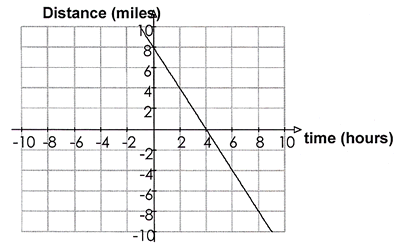 |
(2 pts) y-intercept __________
(2 pts) slope ______________
|
|
| 19. |
Alice bought a new computer for $945. The
computer decreases in value by $35 each month.
Let y = the value of the computer and x
= the number of months since the computer was purchased.
|
| a) (3 pts) Write a linear equation
to represent this situation. Write your final answer in
the form y = mx + b
|
| |
_______________________
|
|
b) (2 pts) After how many months will the value of
the computer be 0 dollars?
|
| |
|
| 20. |
Martha is asked to use the FOIL method to multiply
out (x- 4)(x + 6).
Martha knows that FOIL stands for, "First, Outside, Inside, and Last".
(2 pts) Suppose that Martha did the multiplication
in an order different than suggested by the FOIL
method. Would she still get the same answer as the FOIL method? Circle Yes or No.
(2 pts) Explain your reasoning. If you get the same
answer whether or not you use the FOIL method, why does
the textbook suggest using the FOIL method?
|

