Student Content Assessment
Instrument 28: Pre-electronic ITS Evaluation System
Project: Case-Based Reasoning for Engineering Statistics
Arizona State University
Funding Source: NSF - Division of Undergraduate Education (DUE)
Purpose: To evaluate the effectiveness of practice-problems for an upcoming quiz and different methods of preparation (using conditions as close to the actual test situation as possible) for an undergraduate engineering statistical course.
Administered To: Undergraduates who attended an optional study session for the engineering statistics course.
Topics Covered:
- Content Specific Assessment: Engineer-related statistics
Format/Length: 8 open-ended items
Summary of Pre-electronic ITS Evaluation System
Fall, 2002
Preparation
An announcement was made to inform the students of the date and time of the experiment. This announcement can be found in A0.
In preparation for the experiment three primary packets were prepared. One packet consisted of the 6 problems with an example for each problem. The next packet consisted of only the 6 problems. Stapling the six exercises together in a random fashion made each packet. The final products can be found in A 1 and A2. An instruction/debriefing page was then added as the cover. The instruction page for the group with exercises can be found in A 11 and the group without can be found in A21. The problems with examples were labeled an even number and the problems without were labeled an odd number. These two packets were then put together to form one group in numeric order. So when students received their packet they were unaware that there were two different groups.
The third packet consisted of two post problems. Stapling the two exercises in random order made each packet. The final product can be seen in A3. An instruction and debriefing page was then added as the cover, A31. These packets were than randomly put together to form one group.
Solutions to the exercises and post problems along with a debriefing were generated to give to students and the end of the experiment. The debriefing can be found in A4, the solutions to the exercises are A5 and the solutions to the post test are A6.
The Experiment Day
Graduate students along with Dr. Hubele and Dr. Runger proctored the day of the experiment. There were always two individuals proctoring the examples throughout the day. One was in charge of distributing and recording information and the other one was in charge of answering questions after an individual completed the experiment.
When a student entered the room they were given a formula sheet, A7, a numbered packet along with a blue book to complete their work inside of. The proctor recorded their packet number onto the blue book and also recorded the time they distributed the material onto an excel spreadsheet. this excel spreadsheet consisted of the number, time out and in of the exercises, and the time out and in of the post problems. When they completed the exercises, they gave the proctor their exercises and blue book. The proctor recorded the time in and gave them the post problem exercises with their number on it. When they finished the post problem exercises they gave it to the proctor, the proctor then supplied them with the solutions and informed them that there was a graduate student outside available to answer any questions.
ECE 380 ANNOUNCEMENT
There will be a study session for Engineering Statistics on Monday, September 30, 9:00 AM to 9:00 PM in Goldwater Center Room 487. To make it most worthwhile, please anticipate being in the session for about 1.5 hours.
During this study session, you will have an opportunity to work some practice quic problems and get immediate feedback. At the same time, we will be collecting information to help us help you learn statistics.
The instructors are interested in how these sorts of practice sessions affect student performance on quizzes and tests. We will keep track of your performance, and use this information to make changes to the course, the text, and the assignments. We believe that this will help you to learn statistics more effectively, and that it will help other students in the future.
The study session is optional, and open to all students; your grade in the class will not be affected by your attendance, and you can stay as long as you like. If you have any questions about the study session or the research we are doing, please fee free to ask us.
We hope to see you there!
ECE 380 Team
Fall, 2002
Figure A1: Exercises with examples
If the approrpriate assumptions are satisfied,
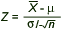
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
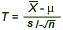
has a t distribution with n-1 degrees of freedom |
EXERCISE: YARN
A textile fiber manufacturer is investigating a new drapery yarn, which the company claims
has a mean elongation force of 14 kg. The company wishes to test the hypothesis that the mean elongatin force is less than 14 kg. The company collects the following sample data: 13.87, 13.85, 13.72, 14.32 which has a sample mean 13.92 and sample standard deviation 0.24. Assuming normality of the data, use  = 0.05 to perform the test. = 0.05 to perform the test.
EXAMPLE: THREAD
A fabric producer is researching a new curtain thread, which the company asserts has a mean breaking strength of 800 g. The manufacturer wants to claim that the mean force is under 800 g. The company records the following data: 795, 790, 775, 825, 780, which has a sample mean 793 and sample standard deviation 19.56. Assuming normality of the data, use  = 0.05 to perform the test. = 0.05 to perform the test.
Solution
- The parameter of interest is
 , the mean breaking strength. , the mean breaking strength.
- H0:
 = 800 g = 800 g
- H1:
 < 800 g < 800 g
 = 0.05 = 0.05
-
The test statistic is
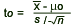
- Reject H0 if t 0 < -t0.05, 4 = -2.132.
- Computation: Since
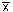 = 793, s = 19.56, = 793, s = 19.56, 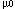 = 800, and n = 5, we have = 800, and n = 5, we have 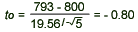
- Conclusion: Since t0=-0.80 > - 2.132, we fail to reject H0 and conclude
that the data do not provide sufficient evidence to show that the mean breaking strength is less
than 800 g.
Figure A11: Debriefing for group with exercises and examples
In this activity, we are going to present you with 6 statistics problems to solve. You will notice that we have given you several aids to help you solve them. At the top of the page are the equations for the t and z test statistics. Also, below each problem to solve, there is a worked example.
This worked exampled is the same kind of problem as the one you are being asked to solve. If you can figure out how the worked example was done, you will be able to reach the correct solution on the problem you are solving. Read both problems carefully, and try to make use of the worked example as much as possible.
Put all of your work in the blue books you have been provided; please do not make any marks in this packet. Show as much of your work as possible, and don't worry about making mistakes, or us seeing your mistakes. If you make an error, don't bother erasing, just draw an X through it and keep going. This is practice; what matters is that you learn how to solve the problems, and we learn how to help you solve the problems. Knowing what you are thinking when you are solving the problems is more important than a neat blue book or hiding your mistakes.
This activity is not graded; you'll notice that we don't even know who you are, you are identified only by a number. So you don't have to worry about us seeing your false starts and mistakes.
Please work through the problems in the order they are given. Do your best with each, but don't get stuck on any one problem. Once you have done all you can on a problem, turn the page and move on. Please do not return to any earlier problems once you have turned the page.
If you have any questions, please feel free to ask us. Otherwise, you may begin. When you are finished, please bring your packet and blue book back up to us.
If the approrpriate assumptions are satisfied,
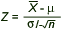
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
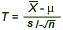
has a t distribution with n-1 degrees of freedom |
EXERCISE: CABLE HARNESS
The diameter of holes for cable harness is known to have a standard deviation of 0.02 in. A random sample of size 10 yields the following data: 1.76, 1.69, 1.74, 1.73, 1.76, 1.77, 1.75, 1.78, and 1.76, with sample mean 1.749. Is the true mean diameter less than 1.75? Use  = 0.01. = 0.01.
EXAMPLE: METAL CORD
The diameter of slots for metal cord tackle is known to have a standard deviation of 0.02 in. A random sample of amount 10 renders the subsequent data: 2.49, 2.44, 2.49, 2.48, 2.51, 2.52, 2.50, 2.53, 2.50, and 2.51, with sample mean 2.497. Is the true mean diameter under 2.50? Use  = 0.01. = 0.01.
Solution
- The parameter of interest is
 , the mean diameter. , the mean diameter.
- H0:
 = 2.50 in = 2.50 in
- H1:
 < 2.50 in < 2.50 in
 = 0.01 = 0.01
- The test statistic is
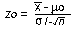
- Reject H0 if Z0 < Z0.01 = -2.32
- Computation: Since
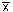 = 2.497, = 2.497, 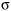 = 0.02, = 0.02, 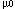 = 2.50, and n = 10, we have = 2.50, and n = 10, we have 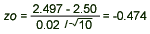
- Conclusion: Since Z0 = -0.474 > -2.32, we fail to reject H0 and conclude that the data do not provide
sufficient evidence to determine that the mean diameter is less than 2.50 in.
If the approrpriate assumptions are satisfied,
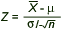
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
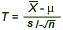
has a t distribution with n-1 degrees of freedom |
EXERCISE: ROCKWELL HARDNESS
The mean Rockwell hardness of a specimen of material is thought to be greater than 60. Five specimens are tested and found to have an average 60.2. The population standard deviation is known to be 0.12. Test the appropriate hyptheses with a significance level  = 0.10. = 0.10.
EXAMPLE: COUPON OF METAL
The mean hardness measurement of a coupon of metal is claimed to be greater than 50. Five coupons are examined and produce an average of 50.3. The population standard deviation is known to be 0.80. Test the appropriate hypotheses with a significance level of 0.10.
Solution
- The parameter of interest is
 , the mean hardness. , the mean hardness.
- H0:
 = 50 = 50
- H1:
 > 50 > 50
-
 = 0.10 = 0.10
- The test statistic is
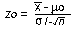
- Reject H0 if Z0 > Z0.10 = 1.28
- Computation: Since
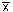 = 50.3, = 50.3, 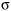 = 0.08, = 0.08, 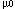 = 50, and n = 5, we have = 50, and n = 5, we have 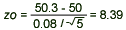
- Conclusion: Since z0=8.39 > 1.28, we reject H0 and conclude that the mean hardness is greater than 50.
If the approrpriate assumptions are satisfied,
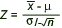
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
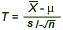
has a t distribution with n-1 degrees of freedom |
EXERCISE: CEREAL MANUFACTURER
A cereal manufacturer requires that the mean weight of a box be more than 20 ounces of cereal. The content of a sample of ten boxes has an average weight 20.15 and standard deviation 0.15 ounces of cereal. Assuming that the weight of the cereal is a normally distributed random variable, test if the mean weight is greater than 20 ounces with a significance level of  = 0.05. = 0.05.
EXAMPLE: GRAIN PRPODUCER
A grain producer demands that the mean weight of a bag be above 32 ounces of grain. The weight of a sample of ten bags has an average weight 32.1 and standard deviation 0.12 ounces of grain. Assuming that the weight of the train is a normally distributed random variable, test if the mean weight is above 32 ounces with a significance level  = 0.05. = 0.05.
Solution
- The parameter of interest is
 , the mean weight. , the mean weight.
- H0:
 = 32 ounces = 32 ounces
- H1:
 > 32 ounces > 32 ounces
 = 0.05 = 0.05
- The test statistic is
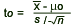
- Reject H0 if t0 > - t0.05, 9 = 1.833
- Computation: Since
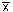 = 32.1, s = 0.12, = 32.1, s = 0.12, 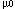 = 32, and n = 10, 23 have = 32, and n = 10, 23 have 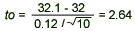
- Conclusion: Since t0 = 2.64 > 1.833, we reject H0 and conclude that the mean weight is more than 32 ounces.
If the approrpriate assumptions are satisfied,
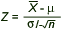
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
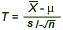
has a t distribution with n-1 degrees of freedom |
EXERCISE: BEVERAGE MACHINE
A post-mix beverage machine is adjusted to release a certain amount of syrup into a chamber where it is mixed with carbonated water. A random sample of 25 beverages was found to have a mean syrup content of 1.098 fluid ounces and a standard deviation of 0.016 fluid ounces. Do the data presented support the claim that the mean amount of syrup dispensed is not 1.0 fluid ounce? Assuming normality of the data, use  = 0.01. = 0.01.
EXAMPLE: SOFT DRINK MACHINE
A soft drink mixing device is modified to discharge a particular quantity of syrup into a container where it is combined with carbonated water. A random sample of 25 servings was determined to have a mean syrup composition of 0.068 fluid ounces and a standard deviation of 0.008 fluid ounces. Is there evidence ot claim the mean quantity of syrup dispensed is different from 0.050 fluid ounces? Assuming normality of the data, use  = 0.01. = 0.01.
Solution
- The parameter of interest is
 , the mean quantity of syrup dispensed. , the mean quantity of syrup dispensed.
- H0:
 = 0.050 fluid ounces = 0.050 fluid ounces
- H1:
 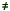 0.050 0.050
 = 0.01 = 0.01
- The test statistic is
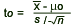
- Reject H0 if t0 < = t0.005, 24 = -2.797 or t0 > t0.005, 24 = 2.797
- Computation: Since
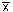 = 0.068, s = 0.008, = 0.068, s = 0.008, 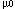 = 0.05, and n = 25, we have = 0.05, and n = 25, we have 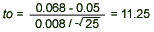
- Conclusion: Since t0 = 11.25 > 2.797, we reject H0, we reject H0 and conclude that the mean quantity of syrup is different from 0.050 fluid ounces.
Figure A21: Instructions for group without examples
In this activity, we are going to present you with 6 statistics problems to solve. You will notice that we have given you aids to help you solve them. At the top of the page are the quations for the t and the z tests.
Put all of your work in the blue books you have been provided; please do not make any marks in this packet. Show as much of your work as possible, and don't worry about making mistakes, or us seeing your mistakes. If you make an error, don't bother erasing, just draw an X through it and keep going. This is practice; what matters is that you learn how to solve the problems, and we learn how to help you solve the problems. Knowing what you are thinking when you are solving the problems is more important than a neat blue book or hiding your mistakes.
This activity is not graded; you'll notice that we don't even have who you are, you are identified only by a number. so you don't have to worry about us seeing yoru false starts and mistakes.
Please work through the problems in the order they are given. Do your best with each, but don't get stuck on any one problem. Once you have done all you can on a problem, turn the page and move on. Please do not return to any earlier problems once you have turned the page.
If you have any questions, please feel free to ask us. Otherwise, you may begin. When you are finished, please bring your packet and blue book back up to us.
If the approrpriate assumptions are satisfied,
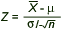
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
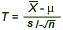
has a t distribution with n-1 degrees of freedom |
EXERCISE: YIELD
The yield of a chemical process is being studied. From previous experience with this process the standard deviation of teh yield is known to be 3. The past 5 days of plant operation have resulted in the following yields: 91.6%, 88.75%, 90.8%, 89.95%, and 91.3%. The sample mean is calculated as 90.48%. Is there evidence that the mean yield is not 90%? Use  = 0.10. = 0.10.
EXAMPLE: PRODUCT
The product of a chemical procedure is being analyzed. From prior studies with this procedure the standard deviation of the product is known to be 2.5. The last 5 days of factory production have generated the subsequent products: 99.7%, 96.75%, 98.80%, 97.90%, and 99.30%. The sample mean is calculated as 98.49%. Can the company conclude that the mean is different from 98%? Use  = 0.10. = 0.10.
Solution
- The parameter of interest is
 , the mean product. , the mean product.
- H0:
 = 98% = 98%
- H1:
 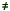 98% 98%
 = 0.10 = 0.10
- The test statistic is
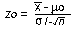
- Reject H0 if Z0 > Z0.05 = 1.65 or if Z0 < -Z0.05 = -1.65
- Computation: Since
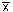 = 98.49%, = 98.49%, 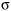 = 2.5%, = 2.5%,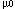 = 98%, and n = 5, we have = 98%, and n = 5, we have 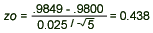
- Conclusion: Since Z0 = 0.438 < 1.65 and Z0 = 0.438 > -1.65, we fail to reject H0 and conclude that the data do not provide sufficient evidence to determine that the mean product is not equal to 98%.
Figure A2: Exercises without examples
If the approrpriate assumptions are satisfied,
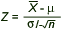
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
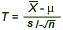
has a t distribution with n-1 degrees of freedom |
EXERCISE: YARN
A textile fiber manufacturer is investigating a new drapery yarn, which the company claims
has a mean elongation force of 14 kg. The company wishes to test the hypothesis that the mean
elongatin force is less than 14 kg. The company collects the following
sample data: 13.87, 13.85, 13.72, 14.32, 13.92 which has a sample mean 13.92 and sample
standard deviation 0.24. Assuming normality of the data,
use  = 0.05 to perform the test. = 0.05 to perform the test.
If the approrpriate assumptions are satisfied,
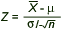
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
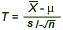
has a t distribution with n-1 degrees of freedom |
EXERCISE: BEVERAGE MACHINE
A post-mix beverage machine is adjusted to release a certain amount of syrup into a chamber
where it is mixed with carbonated water. A random sample of 25 beverages was found to have a
mean syrup content of 1.098 fluid ounces and a standard deviation of 0.016 fluid ounces. Do
the data presented support the claim that the mean amount of syrup dispensed is not 1.0 fluid
ounce? Assuming normality of the data, use  = 0.01. = 0.01.
If the approrpriate assumptions are satisfied,
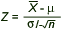
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
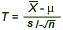
has a t distribution with n-1 degrees of freedom |
EXERCISE: CEREAL MANUFACTURER
A cereal manufacturer requires that the mean weight of a box be more than 20 ounces of cereal.
The content of a sample of ten boxes has an average weight 20.15 and standard deviation 0.15
ounces of cereal. Assuming that the weight of the cereal is a normally distributed random
variable, test if the mean weight is greater than 20 ounces with a significant level  = 0.05. = 0.05.
If the approrpriate assumptions are satisfied,
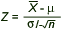
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
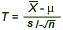
has a t distribution with n-1 degrees of freedom |
EXERCISE: ROCKWELL HARDNESS
The mean Rockwell hardness of a specimen of material is thought to be greater than 60.
Five specimens are tested and found to have an average 60.2. The population standard deviation is
known to be 0.12. Test the appropriate hyptheses with a significance level  = 0.10. = 0.10.
If the approrpriate assumptions are satisfied,
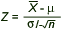
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
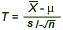
has a t distribution with n-1 degrees of freedom |
EXERCISE: CABLE HARNESS
The diamter of holes for cable harness is known to have a standard deviation of 0.02 in.
a random sample of size 10 yields the following data: 1.76, 1.69, 1.74, 1.73, 1.76, 1.77, 1.75, 1.78, 1.75, and 1.76,
with sample mean 1.749. Is the true mean diameter less than 1.75?
Use  = 0.01. = 0.01.
If the approrpriate assumptions are satisfied,
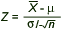
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
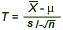
has a t distribution with n-1 degrees of freedom |
EXERCISE: YIELD
The yield of a chemical process is being studied. From previous experience with this process
the standard deviation of the yield is known to be 3. The past 5 days of plant operation have
resulted in the following yields: 91.6%, 88.75%, 90.8%, 89.95%, and 91.3%. The sample mean is
calculated as 90.48%. Is there evidence that the mean yield is not 90%? Use  = 0.10. = 0.10.
Figure A3: Post Test Problem
If the approrpriate assumptions are satisfied,
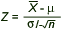
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
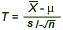
has a t distribution with n-1 degrees of freedom |
EXERCISE: VOLTAGE
A sample of 10 breakdown voltages, ud, of coaxial insulation are recorded
and found to have an average of 148 kV and a standard deviation of 2.5 kV. The power company
would like to determine if the mean breakdown voltage is 150 kV. use a significance level of
0.05.
If the approrpriate assumptions are satisfied,
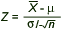
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
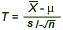
has a t distribution with n-1 degrees of freedom |
EXERCISE: VISCOSITY
According to the engineering specification, a chemical process is designed to generate a
fluid with a viscosity greater than 10.2 Pa s (Pascal seconds). The standard deviation of
viscosity is known to be 0.5 Pa s. A sample of 20 batches of the fluid yields an average
viscosity measurement of 10.23. Based on the sample data, does the process conform to the
engineering specification? Use  = 0.10. = 0.10.
A31: Debriefing for Post Problems
Now that you have had a chance to practice the problems, we'd like you to do some post-tutorial
problems. This will provide you with a "dress rehearsal" for some of the quiz problems
that you wil take in class this week.
There are just 2 problems in this packet. Put all of your work in the blue books you have
been provided; please do not make any marks in the packet. show as much of your work as
possible, and don't worry about making mistakes, or us seeing your mistakes. If you make
an error, don't bother erasing, just draw an X through it and keep going.
Once you have finished this exercise, you will be given a packet with complete step-by-step
solutions. Also, we will return a copy of your post-tutorial exercises to you fully graded
just as it would be in class. This will help you understand how we evaluate the problems.
IMPORTANT: Remember your id number--we don't know who is who, so to pick up your results,
you have to have your id number!
Please work through the problems in the order they are given. do your best with each,
but don't get stuck on any one problem. Once you have done all you can on a problem, turn
the page adn go on to the second.
If you have any questions, please feel free to ask us. Otherwise, you may begin. When you
are finished, please bring your packet and blue book back up to us.
Figure A3: Post Problems
If the approrpriate assumptions are satisfied,
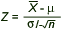
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
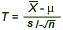
has a t distribution with n-1 degrees of freedom |
EXERCISE: VOLTAGE
A sample of 10 breakdown voltages, ud, of coaxial insulation are
recorded and found to have an average of 148 kV and a standard deviation of 2.5 kV. The power
company would like to determine if the mean breakdown voltage is 150 kV. use a significance
level of 0.05.
If the approrpriate assumptions are satisfied,
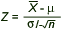
has a standard normal distribution N(0,1) |
If the appropriate assumptions are satisfied,
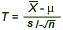
has a t distribution with n-1 degrees of freedom |
EXERCISE: VISCOSITY
According to the engineering specification, a chemical process is designed to generate a
fluid with a viscosity greater than 10.2 Pa s (Pascal seconds). The standard deviation of
viscosity is known to be 0.5 Pa s. A sample of 20 batches of the fluid yields an average
viscosity measurement of 10.23. Based on the sample data, does the process conform to the
engineering specification? Use  = 0.10. = 0.10.
Figure A4: Solution Debriefing
Debriefing
Important: We hope that these exercises have been helpful in partial
preparation for your upcoming Quiz 2. However, please be informed that you can expect to see
other types of questions and topics on the quiz.
This booklet contains complete solutions to all of the problems, both the practice
exercises and the practice post-tutorial exercises. This is yours to take home and study from.
Don't forget to write your id number on here as a reminder! Otherwise, you won't be able to
get your graded post-tutorial exercises back!
The purpose of this study session was two-fold: First, we wanted to give you a chance to
prepare for the upcoming quiz by working problems in a situation that is close to the actual
test conditions. Psychologists have shown that learning is very depedent on context; the closer
the practice conditions are to the test conditions, the better peopl do on the test. So, we hope
this will help you when you take the real quiz!
Second, we also wanted to know how different kinds of practice work. That is why different
people received types of practice problems. From the perspective of how our minds process
information, we really don't know how these different types of practice work. They may even
be exactly the same. We do know that all practice is helpful, so everyone who came should
benefit from attending this session.
Because we are trying to do research on how practice methods work, we need your help. Please
do not discuss the study session with students who have not yet attended. At the end of the day,
all of the study sessions will be over, and you can share these packets and your thoughts all you
like. But until then, please keep this packet and your ideas about the session to yourself.
Thank you for understanding.
If you have any questions, just ask, or you get in touch with us. Good luck on the quiz!
We hope this helped you!
Figure A5: Solutions to Exercises
EXERCISE: YARN
A textile fiber manufacturer is investigating a new drapery yarn, which the company claims has a mean elongation force of 14 kg. The company wishes to test the hypothesis that the mean elongatin force is less than 14 kg. The company collects the following sample data: 13.87, 13.85, 13.72, 14.32, 13.92 which has a sample mean 13.92 and sample standard deviation 0.24. Assuming normality of the data, use  = 0.05 to perform the test. = 0.05 to perform the test.
Solution
- The parameter of interest is
 , the mean elongation force. , the mean elongation force.
- H0:
 = 14 kg = 14 kg
- H1:
 < 14 kg < 14 kg
 = 0.05 = 0.05
- The test statistic is
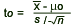
- Reject H0 if t0 < -t0.05, 4 = -2.132.
- Computation: Since
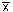 = 13.92, s = 0.24, = 13.92, s = 0.24, 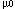 = 14, and n = 5, we have = 14, and n = 5, we have 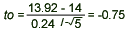
- Conclusion: Since t0 = -0.75 > -2.132, we fail to reject H0 and conclude
that the data do not provide sufficient evidence to show that the mean breaking strength is less than
14 kg.
EXAMPLE: THREAD
A fabric producer is researching a new curtain thread, which the company asserts has a mean breaking strength of 800 g. The manufacturer wants to claim that the mean force is under 800 g. The company records the following data: 795, 790, 775, 825, 780, which has a sample mean 793 and sample standard deviation 19.56. Assuming normality of the data, use to  = 0.05 perform the test. = 0.05 perform the test.
Solution
- The parameter of interest is of interest is
 , the mean breaking strength. , the mean breaking strength.
- H0:
 = 800 g = 800 g
- H1:
 < 800 g < 800 g
 = 0.05 = 0.05
- The test statistic is
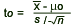
- Reject H0 if t0 < -t0.05, 4 = -2.132.
- Computation: Since
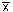 = 793, s = 19.56, = 793, s = 19.56, 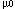 = 800, and n = 5, we have = 800, and n = 5, we have 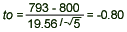
- Conclusion: Since t0= -0.80 > - 2.132, we fail to reject H0 and conclude that the data do not provide sufficient evidence to show that the mean breaking strength is less than 800 g.
EXERCISE: BEVERAGE MACHINE
A post-mix beverage machine is adjusted to release a certain amount of syrup into a chamber where it is mixed with carbonated water. A random sample of 25 beverages was found to have a mean syrup content of 1.098 fluid ounces and a standard deviation of 0.016 fluid ounces. Do the data presented support the claim that the mean amount of syrup dispensed is not 1.0 fluid ounce? Assuming normality of the data, use  = 0.01. = 0.01.
Solution
- The parameter of interest is
 , the mean quantity of syrup dispensed. , the mean quantity of syrup dispensed.
- H0:
 = 1.0 fluid ounces = 1.0 fluid ounces
- H1:
 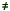 1.0 1.0
 = 0.01 = 0.01
- The test statistic is
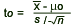
- Reject H0 if t0 < -t0.005, 24 = -2.797 or t0 > t0.005, 24 = 2.797
- Computation: Since
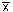 = 1.098, s = 0.016, = 1.098, s = 0.016, 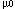 = 0.05, and n = 25, we have = 0.05, and n = 25, we have 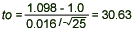
- Conclusion: Since t0 = 30.63 > 2.797, we reject H0 and conclude that the mean
quantity of syrup is different from 1.0 fluid ounces.
EXAMPLE: SOFT DRINK MACHINE
A soft drink mixing device is modified to discharge a particular quantity of syrup into a container where it is combined with carbonated water. A random sample of 25 servings was determined to have a mean syrup composition of 0.068 fluid ounces and a standard deviation of 0.008 fluid ounces. Is there evidence to claim the mean quantity of syrup dispensed is different from 0.050 fluid ounces? Assuming normality of the data, use  = 0.01. = 0.01.
Solution
- The parameter of interest is
 , the mean quantity of syrup dispensed. , the mean quantity of syrup dispensed.
- H0:
 = 0.050 fluid ounces = 0.050 fluid ounces
- H1:
 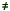 0.050 0.050
 = 0.01 = 0.01
- The test statistic is
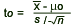
- Reject H0 if t0 < - t0.005, 24 = -2.797 or t0 > t0.005, 24 = 2.797
- Computation: Since
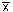 = 0.068, s = 0.008, = 0.068, s = 0.008, 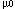 = 0.05, and n = 25, we have = 0.05, and n = 25, we have 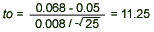
- Conclusion: Since t0 = 11.25 > 2.797, we reject H0 and conclude that the
mean quantity of syrup is different from 0.050 fluid ounces.
EXERCISE CEREAL MANUFACTURER
A cereal manufacturer requires that the mean weight of a box be more than 20 ounces of cereal. The content of a sample of ten boxes has an average weight 20.15 and standard deviation 0.15 ounces of cereal. Assuming that the weight of the cereal is a normally distributed random variable, test if the mean weight is greater than 20 ounces with a significance level of  = 0.05. = 0.05.
Solution
- The parameter of interest is
 , the mean weight. , the mean weight.
- H0:
 = 20 ounces = 20 ounces
- H1:
 > 20 ounces > 20 ounces
 = 0.05 = 0.05
- The test statistic is
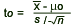
- Reject H0 if t0 > t0.05, 9 = 1.833
- Computation: Since
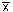 = 20.15, s = 0.15, = 20.15, s = 0.15, 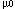 = 20, and n = 10, we have = 20, and n = 10, we have 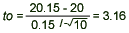
- Conclusion: Since t0 = 3.16 > 1.833, we reject H0 and conclude that the mean weight is more than 20 ounces.
EXAMPLE: GRAIN PRODUCER
A grain producer demands that the mean weight of a bag be above 32 ounces of grain. The weight of a sample of ten bags has an average weight 32.1 and standard deviation 0.12 ounces of grain. Assuming that the weight of the grain is a normally distributed random variable, test if the mean weight is above 32 ounces with a significance level  = 0.05. = 0.05.
Solution
- The parameter of interest is
 , the mean weight. , the mean weight.
- H0:
 = 32 ounces = 32 ounces
- H1:
 > 32 ounces > 32 ounces
 = 0.05 = 0.05
- The test statistic is
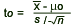
- Reject H0 if t0 > t0.05, 9 = 1.833
- Computation: Since
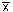 = 32.1, s = 0.12, = 32.1, s = 0.12, 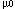 = 32, and n = 10, we have = 32, and n = 10, we have 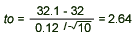
- Conclusion: Since t0 = 2.64 > 1.833, we reject H0 and conclude that the mean weight is more than 32 ounces.
EXERCISE: ROCKWELL HARDNESS
The mean Rockwell hardness of a specimen of material is thought to be greater than 60. Five specimens are tested and found to have an average 60.2. The population standard deviation is known to be 0.12. Test the appropriate hyptheses with a significance level  = 0.10. = 0.10.
Solution
- The parameter of interest is
 , the mean Rockwell hardness. , the mean Rockwell hardness.
- H0:
 = 60 = 60
- H1:
 > 60 > 60
 = 0.10 = 0.10
- The test statistic is
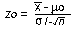
- Reject H0 if Z0 > Z0.10 = 1.28
- Computation: Since
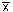 = 60.2, = 60.2, 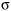 = 0.12, = 0.12, 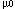 = 60, and n = 5, we have = 60, and n = 5, we have 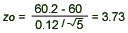 - Conclusion: since z0 = 3.73 > 1.28, we reject H0 and conclude that the mean Rockwell hardness is greater than 60.
EXAMPLE: COUPON OF METAL
The mean hardness measurement of a coupon of metal is claimed to be greater than 50. Five coupons are examined and produce an average of 50.3. The population standard deviation is known to be 0.80. Test the appropriate hypotheses with a significance level of 0.10.
Solution
- The parameter of interest is
 , the mean hardness. , the mean hardness.
- H0:
 = 50 = 50
- H1:
 > 50 > 50
 = 0.10 = 0.10
- The test statistic is
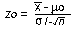
- Reject H0 if Z0 > Z0.10 = 1.28
- Computation: Since
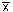 = 50.3, = 50.3, 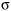 = 0.08, = 0.08, 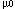 = 50, and n = 5, we have = 50, and n = 5, we have 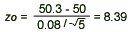
- Conclusion: Since z0=8.39 > 1.28, we reject H0 and conclude that the mean hardness is greater than 50.
EXERCISE: CABLE HARNESS
The diamter of holes for cable harness is known to have a standard deviation of 0.02 in. A random sample of size 10 yields the following data: 1.76, 1.69, 1.74, 1.73, 1.76, 1.77, 1.75, 1.78, 1.75, and 1.76, with sample mean 1.749. Is the true mean diameter less than 1.75? Use  = 0.01. = 0.01.
Solution
- The parameter of interest is
 , the mean diameter. , the mean diameter.
- H0:
 = 1.75 in = 1.75 in
- H1:
 > 1.75 in > 1.75 in
 = 0.01 = 0.01
- The test statistic is
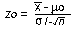
- Reject H0 if Z0 < -Z0.01 = -2.32
- Computation: Since
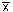 1.749, 1.749, 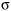 = 0.02, = 0.02, 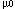 = 1.75, and n = 10, we have = 1.75, and n = 10, we have 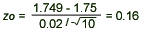
- Conclusion: Since z0 = -0.16 > -2.57, we fail to reject H0 and
conclude that the data do not provide sufficient evidence to determine that the mean diameter
is than 1.75 in.
EXAMPLE: METAL CORD
The diameter of slots for metal cord tackle is known to have a standard deviation of 0.02 in. A random sample of amount 10 renders the subsequent data: 2.49, 2.44, 2.49, 2.48, 2.51, 2.52, 2.50, 2.53, and 2.51, with sample mean 2.497. Is the true mean diameter under 2.50? Use  = 0.01. = 0.01.
Solution
- The parameter of interest is
 , the mean diameter. , the mean diameter.
- H0:
 = 2.50 in = 2.50 in
- H1:
 < 2.50 in < 2.50 in
 = 0.01 = 0.01
- The test statistic is
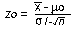
- Reject H0 if Z0 < -Z0.01 = -2.32
- Computation: Since
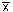 = 2.497, = 2.497, 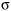 = 0.02, = 0.02, 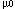 = 2.50, and n = 10, we have = 2.50, and n = 10, we have 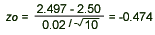
- Conclusion: since Z0 = -0.474 > - 2.57, we fail to reject H0 and conclude that the data do not
provide sufficient evidence to determine that the mean diameter is less than 2.50 in.
EXERCISE: YIELD
The yield of a chemical process is being studied. From previous experience with this process the standard deviation of the yield is known to be 3. The past 5 days of plant operation have resulted in the following yields: 91.6%, 88.75%, 90.8%, 89.95%, and 91.3%. The sample mean is calculated as 90.48%. Is there evidence that the mean yield is not 90%? Use  = 0.10. = 0.10.
Solution
- The parameter of interest is
 , the mean yield. , the mean yield.
- H0:
 = 90% = 90%
- H1:
  = 90% = 90%
 = 0.10 = 0.10
- The test statistic is
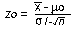
- Reject H0 if Z0 > Z0.05 = 1.65 or if Z0 < -Z0.05 = -1.65
- Computation: Since
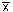 = 90.48%, = 90.48%, 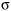 = 3%, = 3%, 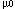 = 90%, and n = 5, we have = 90%, and n = 5, we have 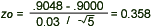
- Conclusion: Since z0 = 0.358 <1.65 and z0 = 0.358 > - 1.65, we fail to
reject H0 and conclude that the data do not provide sufficient evidence to determine
that the mean yield is not equal to 90%.
EXAMPLE: PRODUCT
The product of a chemcial procedure is being analyzed. From prior studies wtih this procedure the standard deviation of the product is known to be 2.5. The last 5 days of factory production have generated the subsequent products: 99.7%, 96.75%, 98.80%, 97.90%, and 99.30%. the sample mean is calculated as 98.49%. Can the company conclude that the mean is different from 98%? Use  = 0.10. = 0.10.
Solution
- The parameter of interest is
 , the mean product. , the mean product.
- H0:
 = 98% = 98%
- H0:
 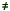 = 98% = 98%
 = 0.10 = 0.10
- The test statistic is
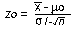
- Reject H0 if Z0 > Z0.05 = 1.65 or if Z0 < -Z0.05 = -1.65
- Computation: Since
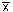 = 98.49%, = 98.49%, 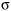 = 2.5%, = 2.5%, 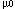 = 98%, and n = 5, we have = 98%, and n = 5, we have 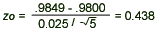
- Conclusion: Since z0 = 0.438 < 1.65 and z0 = 0.438 > - 1.65, we fail
to reject H0 and conclude that the data do not provide sufficient evidence to determine
that the mean product is not 98%.
Figure A6: Solutions to Post Problems
EXERCISE: VOLTAGE
A sample of 10 breakdown voltages ud, of coaxial insulation are recorded and found to have an average of 148 kV and a standard deviation of 2.5 kV. The power company would like to determine if the mean breakdown voltage is 150 kV. use a significance level of 0.05.
Solution
- The parameter of interest is
 , the mean breakdown voltage , the mean breakdown voltage
- H0:
 = 150 kV = 150 kV
- H1:
 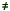 = 150 kV = 150 kV
 = 0.05 = 0.05
- The test statistic is
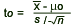
- Reject H0 if t0 < t0.025, 9 = -2.262 or if t0 > t0.025, 9 = 2.262
- Computation: Since
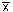 = 148, s = 2.5, = 148, s = 2.5, 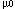 = 150, and n = 10, we have = 150, and n = 10, we have 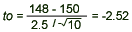
- Conclusion: Since t0 = -2.52 < -2.262, we reject H0 and conclude
that the mean breakdown voltage is less than 150 kV, i.e. different from 150 kV.
EXERCISE: VISCOSITY
According to the engineering specification, a chemical process is designed to generate a fluid with a viscosity greater than 10.2 Pa s (Pascal seconds). The standard deviation of viscosity is known to be 0.5 Pa s. A sample of 20 batches of the fluid yields an average viscosity measurement of 10.23. Based on the sample data, does the process conform to the engineering specification? Use  = 0.10. = 0.10.
Solution
- The parameter of interest is
 , the mean viscosity. , the mean viscosity.
- H0:
 = 10.2 Pa s = 10.2 Pa s
- H1:
 > 10.2 Pa s > 10.2 Pa s
 = 0.10 = 0.10
- The test statistic is
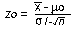
- Reject H0 if Z0 > Z0.10 = 1.282
- Computation: Since
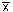 = 10.23, = 10.23, 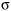 = 0.5, = 0.5, 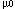 = 10.2, and n = 20, we have = 10.2, and n = 20, we have 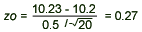
- Conclusion: Since z0 = 0.27 < 1.282, we do not reject H0 and conclude
that the mean viscosity is not more than 10.2 Pa s at a significance level of 0.1, that is, the
process does not conform to specifications.
|
 |

