|
This evaluation viewed the use of the Bridging the Vector Calculus Gap (BVCG) materials from two perspectives — the views of the students involved in the course and, to a lesser extent, the views of the instructors using the materials. We had subjects at two different sites: a medium sized state university (A) and a small liberal arts college (B). We conducted informal interviews with the two instructors at site A and with the graduate teaching assistant who led the labs there. All were enthusiastic about the labs and thought they added to the understanding and interest of their students. One of the instructors said that emphasizing the geometric meaning of vector calculus (both in the labs and in the lectures) makes it much more possible for students to make sense out of what they were doing.
Our investigation of the impact of the lab materials on students was more involved. From the student perspective we evaluated both students' attitudes toward the materials and the nature of their conceptual understanding of the materials. Fifteen students from three different classes were involved in the study -four were from a 10-week "traditional" vector calculus course with three lectures and one recitation per week; four from a 10-week vector calculus course in which the instructor used the BVCG materials in weekly lab classes attached to the course and the instructor made an effort to connect the three weekly lectures to the content of the labs; and seven from a 15-week vector calculus course team taught by the authors of the materials. All participants were volunteers. (We will refer to the group in the "traditional" course as Group T, the group in the l0-week course with labs created by the PIs as Group O and the group in the course taught by the PIs as Group M. The recitations for Group T were designed to answer student's questions on the homework or lecture and to give periodic quizzes. A graduate teaching assistant led these recitations and a different graduate teaching assistant led the Lab sessions for Group O. The authors of the lab materials conducted both lecture and labs for Group M.)
Student volunteers participated in two 45-60 minute task-based interviews - one during first week of their respective vector calculus course and one during the last two weeks of their course. The purpose of the first interview was to give students a task that would allow us to determine in some way their mathematical and visualization abilities at the start of the course, and to determine if our student participant groups were comparable. In the interview we asked students about their educational backgrounds in mathematics; we asked them about their hobbies; and we asked them to construct a graph of:
x2 + y2 + z = 50
There were students in each group who were able to graph this equation and some in each group who were not able to graph the equation. Their methods varied but among the three groups there was no group who, in general, seemed more able than any other group. Further, their mathematics backgrounds were comparable. We thus concluded that none of the three groups seemed to be entering the course with more "ability" than the others.
The purpose of the second interview was to determine the student's attitudes about the course and the attached labs; and to evaluate the effectiveness of the new materials in helping students have a deeper and more diverse understanding of some of the concepts of vector calculus. To determine student attitude, we asked students what things they liked best about their experience in their vector calculus course and if there were any aspects of the course that seemed to be more helpful than others. If students did not mention the recitation (for Group T) or the labs (for Groups O or M) we asked directly if they enjoyed their recitation/lab or found it helpful. Only one student in Group T spontaneously mentioned the recitations as one of the course aspects that he found most helpful. Two students were neutral when asked about the recitations and one student did not find recitations helpful at all.
All four of the students in Group O were quite enthusiastic about the labs. One student said, "[These were] probably the best labs of any math class I've taken here." Another said, "... the lab activities and working with others, extremely helpful... . I absolutely loved the labs ...they were great." In addition, all four students felt that the labs related well to the subject matter in the lectures and helped them understand that material more deeply. All seven of the students in Group M had positive things to say about the lab activities, however two of the students were not terribly enthusiastic one of them preferring to work alone and the other raising issues related to group dynamics.
Most of the second interview was devoted to students engaging in the following task:
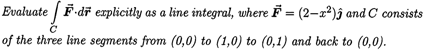
We selected this task because there were a number of ways that the line integral could be evaluated. We believed that it was likely that the method a given student used to solve the problem would reveal his or her understanding of the problem. Only three students got the correct solution - one from each group -however we were more concerned with the method each used and his or her understanding of the concept of line integral.
In Group T, three of the four students begin by parameterizing the curve in terms of t and with varying success tried to evaluate integrals for each line segment in the path. One of these students, for whom this method was successful, went on to apply Stokes' Theorem to verify her answer. The fourth student drew a triangle and labeled it, but was not able to get beyond that point. Interestingly enough, this was the only student who seemed to have more than a vague idea of the meaning of the line integral. In fact, when asked about the meaning of the line integral, the student who was able to get a correct answer by doing the problem in two ways said, "... it means exactly nothing to me other than that [the answer obtained from the first method] matches [the second one]. I mean, ...math classes aren't very integrated to teach you like ...there's not that many story problems anymore."
Each of the four students in Group O, started by drawing the triangle -two of them included the vector field. Three of the four began by reasoning about 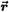 and and 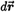 . One student was able to carry these ideas to a successful conclusion and a second student seemed to lose one of his integrals along the way, but would otherwise have been successful. The fourth student tried unsuccessfully to apply Stokes' Theorem. When asked to explain the idea behind line integrals one student said they were "how much you're going with the vector field, how much of the vector field you're experiencing going from point a to point b." Another said it was the work being done going from one point to another. . One student was able to carry these ideas to a successful conclusion and a second student seemed to lose one of his integrals along the way, but would otherwise have been successful. The fourth student tried unsuccessfully to apply Stokes' Theorem. When asked to explain the idea behind line integrals one student said they were "how much you're going with the vector field, how much of the vector field you're experiencing going from point a to point b." Another said it was the work being done going from one point to another.
In some ways Group M is not comparable to the other two groups since their course was five weeks longer, a smaller class, and team taught by the authors. However, looking at the second interviews of this group does give us some valuable information. As a group these students seemed to reason about the line integral task in a more visual way. Four of the seven students, talking about the vector field in relation to the curve reasoned that the integral on the segment from (0,0) to (1,0) would be zero. And two of these students said the integral along the (1,0) to (0,1) segment would be positive and the integral along the (0,1) to (0,0) segment would be negative without doing any computations. All but two students started by saying either that 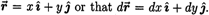 Again, only one of those students carried the task through to a successful end, but only one of the seven seemed completely unable to handle the task. Again, only one of those students carried the task through to a successful end, but only one of the seven seemed completely unable to handle the task.
There are three main conclusions that one can draw from this study. First, the enthusiasm that students had for the lab activities seems important. Students are more likely to engage in mathematics if they enjoy the work and if they find it applicable in their lives (even if it is only seen as applicable to other courses they take). The enthusiasm was possibly more noticeable in the Group O students because there was a greater perception that the lectures and labs were different since they were taught by two different faculty members. However, it is clear that students in the traditional recitation section were not having a comparable experience.
Second, there is some indication that it may be important to integrate more completely the ideas and thinking from the labs into the lecture sections. One of the OSU instructors remarked that given a second opportunity he would emphasize the notion of differentials more in his lectures and examples.
Third, the preparation of instructors to use these materials is important. The use of cooperative groups as well as the innovative way of looking at the mathematics of vector calculus may both be new ideas to faculty, and how well they are prepared to handle these new ideas will be important. |

